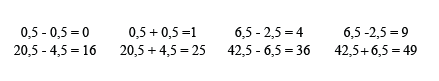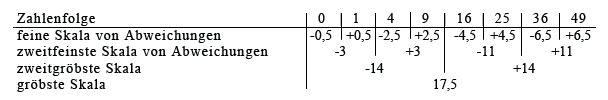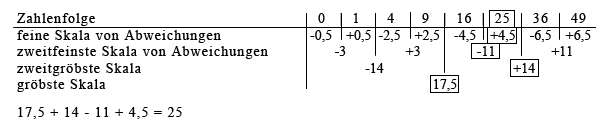Prinzip der Multiskalenanalyse

Musikalische Töne bestehen aus einer Überlagerung einer Vielzahl von Schwingungen. Wie zuvor bereits erläutert, sind nur die Schwingungen mit Frequenzen zwischen etwa 20 und 20.000 Hertz für den Menschen hörbar. Der Faktor zwischen den niedrigsten und den höchsten hörbaren Frequenzen beträgt damit immerhin 1.000 = 10³, also 3 Zehnerpotenzen. Wenn wir also musikalische Töne wieder in die darin enthaltenen Einzelfrequenzen zerlegen wollen, müssen wir ganz unterschiedliche Frequenz-Skalen betrachten. Da die Frequenzen in einem bestimmten Medium wie der Luft in direktem Zusammenhang mit den zugehörigen Wellenlängen stehen (wie in der Gleichung zu Prinzip von MP3 und Grundlagen), können wir ganz analog auch sagen, wir müssen ganz unterschiedliche Skalen von Wellenlängen betrachten. Eine derartige Multiskalenanalyse ist durchaus nicht ungewöhnlich, wenn man die Eigenschaften von Objekten beobachten oder analysieren will.

Anhand von zwei Beispielen wird das Prinzip der Multiskalenanalyse verdeutlicht. Im ersten Beispiel wird eine Multiskalenanalyse durch fortgesetzte Mittelwertbildung für eine gegebene Zahlenfolge durchgeführt. Im zweiten Beispiel betrachten wir die Zerlegung eines Tonsignals in sogenannte Wavelets, was der Zerlegung in Rechteckschwingungen entspricht.

Wir betrachten als Beispiel folgende Zahlenfolge von Quadratzahlen: 0 1 4 9 16 25 36 49. Fassen wir die Zahlen in Paare zusammen und bilden die Mittelwerte dieser Paare, so erhalten wir die Folge 0,5 6,5 20,5 42,5. Fassen wir diese Zahlen ebenfalls wieder zu Paaren zusammen und bilden die Mittelwerte der Paare, so erhalten wir die Folge 3,5 31,5. Für dieses Zahlenpaar haben wir den Mittelwert 17,5. Wir haben jetzt die ursprüngliche Zahlenfolge in mehrere Skalen von Mittelwerten überführt:

Um von einer Mittelwertskala wieder zur vorhergehenden zu gelangen, benötigen wir die Abweichungen der Mittelwerte von den zugehörigen Werten auf der vorigen Skala:

17,5 - 14 = 3,5 beziehungsweise 17,5 + 14 = 31,5

Entsprechend auf der nächstgröberen Skala:

3,5 - 3 = 0,5 3,5 + 3 = 6,5 31,5 - 11 = 20,5 31,5 + 11 = 42,5

Ganz analog können wir auch von der feineren Skala von Mittelwerten zu unserer ursprünglichen Folge zurückkehren:

Zu den ursprünglichen Zahlen zurück kommen wir jetzt, indem wir den Mittelwert auf der gröbsten Skala und die entsprechenden gespeicherten Abweichungen auf allen feineren Skalen einfach addieren. Ein Beispiel: