Multiskalenanalyse mithilfe von Rechteckschwingungen
Tonsignale lassen sich auch in Rechteckschwingungen zerlegen, deren Skala zunehmend gröber wird.
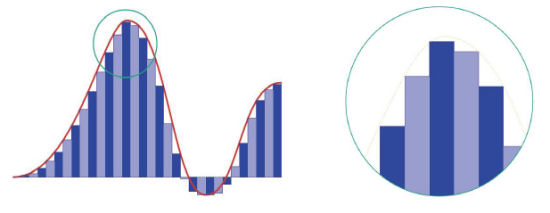
Zerlegung einer Funktion in Rechteckschwingungen
Annäherung an die Funktion durch Balken
Um Tonsignale in Rechteckschwingungen unterschiedlicher Frequenzen zu zerlegen, können wir ganz analog vorgehen. Abb. 9 zeigt links eine Funktion, die wir in Rechteckschwingungen zerlegen wollen. Da wir den Funktionsverlauf in der Praxis oft nicht genau kennen, sondern nur an bestimmten Werten messen, nähern wir die Funktion durch die einzelnen Messwerte an. Diese Messwerte werden durch die gefärbten Balken wiedergegeben.Multiskalenanalyse in beide Richtungen möglich
Auf der rechten Seite der Abbildung 9 ist der umkreiste Ausschnitt der Funktion vergrößert dargestellt. Wir erläutern das Prinzip unserer Multiskalenanalyse im Folgenden anhand dieses Ausschnitts.Vergröberung der Skalen
Die linke Skizze in Abb. 10 zeigt, dass wir wie im vorangegangenen Abschnitt bei der Prinzip der Multiskalenanalyse wieder Mittelwerte der gemessenen Funktionswerte bilden, um auf die nächstgröbere Skala zu kommen. Dieses Vorgehen können wir fortsetzen, um auf gröbere Skalen zu kommen. Die mittlere Grafik von Abb. 10 zeigt den Mittelwert auf der entsprechenden nächstgröberen Skala.Verfeinerung der Skalen
Aber auch die andere Richtung ist denkbar: Zurück zur feinen Skala der Funktion können wir wieder kommen, indem wir wieder die Abweichungen zum Mittelwert hinzu addieren. So erhalten wir wieder die ursprünglichen Messwerte der Funktion zurück. Betrachten wir jetzt die rechte Seite in dieser Abbildung genauer, so stellen wir fest, dass wir tatsächlich unseren Funktionsausschnitt in eine Folge von Rechteckschwingungen zerlegt haben.Abweichungen entsprechen der Rechteckschwingung
Dabei sind wir ganz genauso vorgegangen wie bei der Multiskalenanalyse unserer Zahlenfolgeim vorangegangenen Abschnitt (Prinzip der Multiskalenanalyse). Die Zahlenfolge dort können wir auch auffassen als Messwerte für die Funktion f(x) = x2. Daher haben wir auch dort bereits eine Zerlegung dieser Funktion in Rechteckschwingungen durchgeführt. Dies wird deutlich, wenn wir die Abweichungen auf den einzelnen Skalen nochmals genauer betrachten. Wir stellen dabei fest, dass je zwei dieser Abweichungen den gleichen Betrag haben, sich aber im Vorzeichen unterscheiden; so können z.B. die Werte ?3 und +3 auf der zweitfeinsten Skala von Abweichungen als eine Rechteckschwingung (der Höhe 3) aufgefasst werden.
Download
- mp3_ab5.pdf
In diesem Arbeitsblatt soll eine Funktion in Rechteckschwingungen unterschiedlicher Frequenzen zerlegt werden.
VorschauIm Classroom-Manager speichern
Weiterlesen
- Huffman-Codierung
Um in MP3 die verbliebenen Informationen effizient abzuspeichern, nutzt man die Huffman-Codierung.