Spätestens mit der Entdeckung von SARS-CoV-2 wurde der Epidemiologie als wissenschaftliche Disziplin eine neue Rolle in der Beurteilung des Infektionsgeschehens und des Verständnisses von Infektionskrankheiten zugeschrieben. Gleichzeitig konnte die bereits vor 2020 geäußerte Annahme, dass sich das Auftreten von Pandemien in Zukunft noch deutlich intensivieren würde, bestärkt werden. Die Gründe dafür sind vielfältig und es ist nicht verwunderlich, dass das Forschungsinteresse, Risiken zu identifizieren und Prognosen zu erstellen, wann und wo eine neue Infektionskrankheit auftreten könnte, eine vollkommen neue Gewichtung erhalten hat.
Genau hier setzt die Unterrichtseinheit an und beschäftigt sich mit der Epidemiologie und den ihr zugrundeliegenden Modellen, mit dem Ziel, durch eine angeleitete naturwissenschaftlich-mathematische Modellierung den Infektionsverlauf von SARS-CoV-2 angemessen zu modellieren. In mehreren Zyklen wird hier das sogenannte SIR-Modell entwickelt. Es beschreibt mathematisch die Zusammenhänge zwischen verschiedenen Gruppen mit definierten Gesundheitszuständen und stellt die Lernenden zunächst vor die Herausforderung, dieses Wirkungsgefüge und die Wechsel zwischen den Gesundheitszuständen (als Infektion und Genesung bezeichnet) im Sinne des systemischen Denkens zu erfassen.
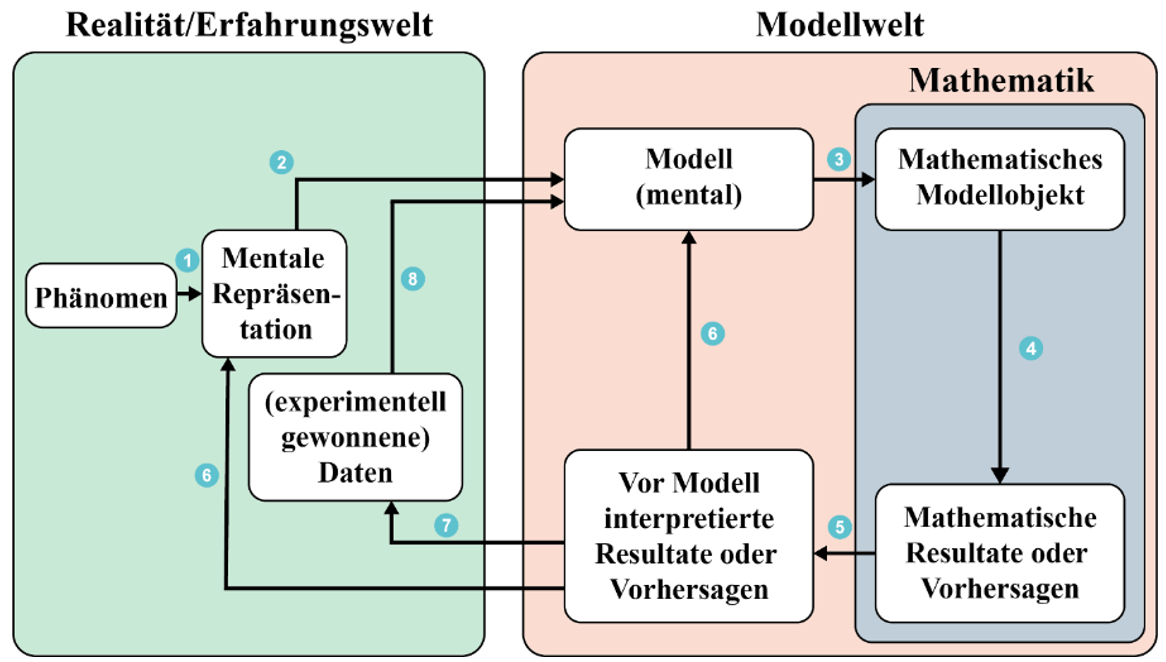
Neben dem fachspezifischen Wissen, welches in beiden Fächern vertieft oder erworben wird, werden durch den permanent eingeforderten Realitätsbezug auch spezielle Gestaltungskompetenzen (siehe BNE) adressiert. Sie sind essenziell bei der Übersetzung und Interpretation der Realität in ein Modell und umgekehrt und befähigen auch in Zukunft zur eigenständigen Durchdringung und Modellierung anderer komplexer Sachverhalte. Gleichzeitig lassen sich nur so Erklärungen für die Entwicklung der Fallzahlen finden und zukünftige Infektionsentwicklungen prognostizieren.
Der fächerübergreifende Charakter der Lerneinheit zwischen Mathematik und Biologie (diese Verortung findet sich auch im Lehrplan wieder) fordert fachliche Vorkenntnisse aus beiden Fächern. Im Fach Biologie zählen dazu grundlegendes biologisches Wissen über die Zelle, die dort ablaufenden Prozesse (Transkription, Translation et cetera) sowie das Basiskonzept des Schlüssel-Schloss-Prinzips. Mathematisches Vorwissen wird im Bereich der Analysis und Differentialrechnung (Differenzenquotient, Steigung/Steigungsdreieck, Ableitung) und der rekursiven Berechnung von einzelnen Werten vorausgesetzt.
Hinweise zu den Download-Materialien
Arbeitsheft: Das Arbeitsheft enthält alle Arbeitsaufträge und leitet durch die Unterrichtseinheit. Eine Vierergruppe erhält zwei Arbeitshefte von Teil 1 und Teil 2. Diese unterscheiden sich nur in bestimmten Aufgaben voneinander und ermöglichen so die Bearbeitung der Lerneinheit als Gruppenpuzzle.
Hilfeheft: Im Hilfeheft finden sich gestaffelte Hilfestellungen, die von den Lernenden eigenständig und nach Bedarf zu Rate gezogen werden können. Jede Vierergruppe erhält ein Hilfeheft Teil 1 und Teil 2.
Weitere Printmaterialien: Diese finden sich alle im Materialordner im Downloadbereich der Station und werden für ihre Bearbeitung benötigt. Jede Gruppe erhält einen Satz aller Printmaterialien.
Digitale Kompetenzen, die Lehrende zur Umsetzung der Einheit benötigen
Die Lehrenden organisieren die digitale Teilhabe aller Lernenden und leiten sie an, die digitale Lerneinheit im Webbrowser aufzurufen und die dort bereits vorkonfigurierten Ressourcen zu nutzen. Sie gewährleisten außerdem, dass die Lernenden über alle erforderliche Vorkenntnisse und Fähigkeiten (sowohl digitale als auch nicht digitale) verfügen (2.3. Organisieren, Schützen und Teilen digitaler Ressourcen, 5.1. Digitale Teilhabe). Die Lerneinheit sollte von den Lehrenden sinnstiftend in den Unterricht eingebettet werden und dementsprechend einerseits unter Berücksichtigung der Lernziele, die ihren Ursprung im fächerübergreifenden Unterricht haben und andererseits des Kontextes der Epidemiologie behandelt werden. Die neu gewonnenen Erkenntnisse sollten zur besseren Integration der Lerneinheit im weiteren Unterrichtsverlauf erneut aufgegriffen, reflektiert und kritisch diskutiert werden. Dabei kann es hilfreich sein, diese Auseinandersetzung in neue Formate oder pädagogische Methoden zu integrieren (3.1. Lehren, 2.1. Auswahl digitaler Ressourcen).
Während der Arbeitsphase begleiten die Lehrenden die Gruppenarbeiten und unterstützen die Lernenden auf verschiedenen Ebenen, sodass selbstgesteuertes Lernen, ein zielgerichteter Umgang mit den digitalen Elementen (vor allem den GeoGebra-Simulationen) und eine individuelle Bearbeitung (eigenes Niveau und eigenes Lerntempo) erreicht werden (3.2. Lernbegleitung, 3.4. Selbstgesteuertes Lernen, 5.2. Differenzierung und Individualisierung). Dazu zählt auch, die Kommunikation, die Teamarbeit und die kollaborative Nutzung der digitalen Medien innerhalb der unterschiedlichen Personenkonstellationen zu initiieren beziehungsweise zu fördern und die Lernenden somit bei Bedarf aktiv in die Arbeitsprozesse einzubinden. Dies gilt vor allem für die Aufgaben, in denen sich die Lernenden in der Stammgruppe über die in den Gruppen aus Expertinnen und Experten erarbeiteten Ergebnisse austauschen (3.2. Lernbegleitung, 3.3. Kollaboratives Lernen, 3.4. Selbstgesteuertes Lernen, 5.3. Aktive Einbindung der Lernenden).
Digitale Medien werden in der Lerneinheit außerdem (von den Lehrenden) eingesetzt, um sich mit vielfältigen Herausforderungen aktiv und kreativ auseinandersetzen zu können. Dementsprechend werden sie zur Förderung der Kommunikation, der Zusammenarbeit in der Gruppe, zur Anregung von Diskussionen und damit zur gemeinsamen Lösungsfindung genutzt (5.3. Aktive Einbindung von Lernenden, 6.2. Digitale Kommunikation und Zusammenarbeit, 6.5. Digitales Problemlösen).
Vermittelte Kompetenzen
Fachkompetenz
Die Schülerinnen und Schüler
- stellen die Epidemiologie als interdisziplinäres Fachgebiet dar, indem sie verschiedene Methoden dieses Gebietes anwenden.
- erläutern verschiedene Modelle, indem sie die mathematischen Eigenschaften, die Einflüsse verschiedener Parameter und die Zusammenhänge zwischen einzelnen Größen qualitativ untersuchen.
- interpretieren mathematisch gewonnene Ergebnisse durch Rückbezug zur Realität und initiieren so neue Modellierungszyklen.
Medienkompetenz
Die Schülerinnen und Schüler
- sind in der Lage, die Informationen aus den zur Verfügung gestellten digitalen Materialien zu analysieren, interpretieren und zu nutzen.
- verarbeiten Informationen, Inhalte und vorhandene digitale Produkte weiter und integrieren diese in bestehendes Wissen.
- lernen GeoGebra als digitales Mathematikwerkzeug kennen und wenden es in vorgegebenen Aktivitäten zur qualitativen Betrachtung von Modellierungsprozessen an.
Sozialkompetenz
Die Schülerinnen und Schüler
- dokumentieren Überlegungen, Lösungswege beziehungsweise Ergebnisse gemeinsam, stellen sie verständlich dar und präsentieren sie, auch unter Nutzung geeigneter Medien.
- erfahren (unter anderem durch die Konstellationen im Gruppenpuzzle), dass jede/jeder ihre/seine individuellen Stärken einbringen kann.
- reflektieren, dass gelungene Kooperation und Kommunikation zu einem gemeinsamen inhaltlichen Ergebnis führen können.
21st Century-Skills
Die Schülerinnen und Schüler
- können Zusammenhänge qualitativ untersuchen, verbal und grafisch beschreiben und systematisieren.
- erschließen komplexe Themengebiete mithilfe von Gestaltungskompetenzen eigenständig.
- interpretieren Modelle und leiten Schlussfolgerungen für die Realität und zukünftiges Handeln ab.
Literaturhinweise
Meister, J. & Upmeier zu Belzen, A. (2018): Naturwissenschaftliche Phänomene mit Liniendiagrammen naturwissenschaftlich-mathematisch model-lieren. In: M. Hammann & M. Lindner (Hrsg.), Lehr- und Lernforschung in der Biologiedidaktik: Band 8. 2017 (S. 87–106). Studien Verlag, Halle-Wittenberg.