Voraussetzungen, Ablauf der Unterrichtseinheit, Materialien
Die vorliegende Lerneinheit ist zum selbstständigen Arbeiten am Computer konzipiert. Das individuelle Lernen wird durch verschiedene interaktive Elemente unterstützt. So gibt es ein Hilfesystem in Form von Tipps, die sich jeweils hinter einer Glühlampe verbergen. Mögliche Lösungen der Aufgaben sind per Hyperlink auf der Aufgabenseite zu erreichen. Damit ist eine effektive Selbstkontrolle möglich.
Lernvoraussetzungen
Als Lernvoraussetzungen sind grundlegende Kenntnisse im Umgang mit einer Tabellenkalkulation notwendig, wie zum Beispiel die Eingabe von Rechenoperationen. Weiterführende Kenntnisse, wie das Erzeugen von Zufallszahlen, werden nicht vorausgesetzt. Diese können selbstständig erarbeitet werden.
Ablauf der Unterrichtseinheit
Erarbeitung der notwendigen Kenntnisse im Umgang mit EXCEL
Auf der Start-Seite der interaktiven Lerneinheit werden die Schülerinnen und Schüler nach ihren Excel-Kenntnissen gefragt. Je nach Antwort werden sie mit Hyperlinks weiter geleitet. Nach entsprechender Auswahl können die Schülerinnen und Schüler die Eingabe von Zufallszahlen und die Eingabe von Wenn-Funktionen erlernen beziehungsweise bereits Bekanntes vertiefen. Auch steht eine weitere zielorientierte Übung zur VerfügungZentrale Problemstellung
Die Einführung in die Monte-Carlo-Methode erfolgt an Hand der näherungsweisen Bestimmung des Flächeninhalts eines Kreises mit einem Radius Eins. Dazu steht den Schülerinnen und Schülern ein ausführliches Aufgabenblatt zur Verfügung. Unterstützt werden sie unter anderem durch ein interaktives Schaubild, nach dem Erzeugen der Zufallspunkte erscheinen diese auch im Schaubild.
Aufgaben zum selbstständigen Arbeiten
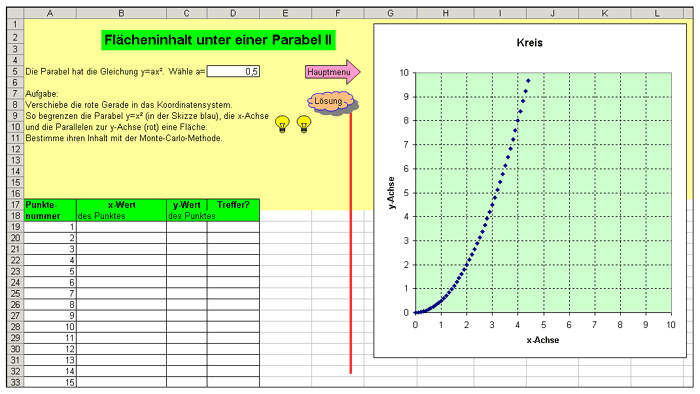
Zur weiteren Vertiefung der Monte-Carlo-Methode stehen noch sechs weitere Aufgabenblätter zur Verfügung. Die ersten beiden Aufgabenblätter vertiefen die näherungsweise Bestimmung des Flächeninhalts eines Kreises. Des Weiteren wird der Vergleich mit dem algebraischen Ergebnis thematisiert. Die beiden folgenden Arbeitsblätter behandeln die Thematik "Flächeninhalt unter einer Geraden", wobei auch hier der Vergleich mit dem algebraischen Ergebnis möglich ist. Die letzten beiden Aufgabenblätter geben schon einen kleinen Einblick in die Integralrechnung, denn die Schülerinnen und Schüler sollen den Flächeninhalt unter einer Parabel bestimmen (Abb. 1, Platzhalter bitte anklicken). An dieser Stelle wird die Notwendigkeit der Monte-Carlo-Methode richtig plastisch: Die Lernenden sind durch diese Methode in der Lage, einen Flächeninhalt näherungsweise zu bestimmen, den sie algebraischen noch nicht berechnen können.
Excel-Materialien
Makros aktivieren
Damit alle eingebauten Funktionen genutzt werden können, müssen bei Excel die Makros aktiviert werden. Vor dem Öffnen der Datei muss dazu im Menü "Extras/Optionen", auf der Registerkarte die Makrosicherheit mindestens auf "mittel" gestellt werden.Dateien mit und ohne Blattschutz
Die erste Tabelle (monte_carlo.xls) ist so angelegt, dass die Lehrperson diese komplett ändern kann. Allerdings können auch die Lernenden Dinge verändern, die sie eigentlich nicht ändern sollten. Die zweite Tabelle (monte_carlo_schutz.xls) ist mit dem für Excel üblichen Blattschutz teilweise geschützt, das heißt die Schülerinnen und Schüler können nur auf gewissen Feldern Eintragungen vornehmen, die nicht geschützt sind.Download
- monte_carlo.xls
Interaktive Arbeitsblätter zur Unterrichtseinheit als Excel-Arbeitsmappe ohne Blattschutz
Im Classroom-Manager speichern - monte_carlo_schutz.xls
Interaktive Arbeitsblätter zur Unterrichtseinheit als Excel-Arbeitsmappe mit Blattschutz
Im Classroom-Manager speichern
Literatur
Dopfer, G., Reimer, R.
Tabellenkalkulation im Mathematikunterricht, Klett Verlag, Stuttgart 1995Engel, A.
Wahrscheinlichkeitsrechnung und Statistik, Band 1, Klett Studienbücher, Stuttgart 1973Hermann, D.
Monte-Carlo-Integration, in: Stochastik in der Schule, 12 (1), 1992, Seite 18-27
Zurück
- Zur Startseite des Beitrags
Bestimmung von Flächeninhalten mit der Monte-Carlo-Methode