Inhalte und Einsatz der Unterrichtseinheit "Die Erde im Radar"
Hier erhalten Sie Hinweise zum Aufbau der Lernumgebung. Die Abbildungen veranschaulichen die Funktionen und die interaktiven Übungen zu den Themenfeldern "Mikrowellen" und "Radarfernerkundung".
Aufbau und Einsatz der Lernumgebung
Computereinsatz und technische Voraussetzungen
Die Unterrichtseinheit bedient sich der Möglichkeiten des Computers, um die Thematik durch Animation und Interaktion zu vermitteln. Den Lernenden wird der Computer nicht als reines Informations- und Unterhaltungsgerät, sondern als nützliches Werkzeug nähergebracht. Die interaktive Lernumgebung ist ohne weiteren Installationsaufwand lauffähig. Auf Windows-Rechnern wird das Modul durch Ausführen der Datei "Mikrowellen_aus_dem_ All.exe". Unter anderen Betriebssystemen wird die Datei "Mikrowellen_aus_dem_ All.html" in einem Webbrowser geöffnet. Hierfür wird der Adobe Flash Player benötigt. Wichtig ist in beiden Fällen, dass die heruntergeladene Ordnerstruktur erhalten bleibt.
Eigenschaften und Nutzerführung
Der jeweils aktivierte Bereich wird auf der unteren Leiste der Lernumgebung eingeblendet (Abb.1). Während der erste Teil einen Einblick in die Thematik liefert und eine übergeordnete Aufgabenstellung benennt, gliedert sich der Rest des Moduls in zwei Sequenzen: Der erste Teil bietet Hintergrundinformationen zum Thema. Im zweiten Teil werden die Schülerinnen und Schüler aktiv und wenden eigenständig Bildbearbeitungsmethoden zur Lösung von entsprechenden Aufgaben an. Den Abschluss eines jeden Bereichs bildet ein Quiz. Erst nach dem Bestehen dieser kleinen Übung wird der folgende Teil der Lernumgebung zugänglich und erscheint in der Seitenleiste. Danach ist auch ein Springen zwischen den Teilbereichen möglich.
Inhalte im Überblick
1. Einleitung
Nach dem Start des Lernmoduls sehen die Schülerinnen und Schüler einen Einführungskasten, der kurz in das Thema Radar einleitet und den Aufbau der Lernsequenz erklärt. Das Bild des Mackenzie-Flusses zeigt bereits eine Anwendungsmöglichkeit der Radarfernerkundung auf.
Der erste Teil des Lernmoduls legt als Hintergrundwissen die Grundlagen für die spätere Arbeit mit den Satellitenbildern im zweiten Modulteil. Dieser Teil besteht aus zwei Rubriken. "Radarfernerkundung" (1) und "Radardaten" (2). In Kapitel 1 erfahren die Schülerinnen und Schüler zunächst Grundsätzliches über Radarsysteme und die verwendeten Wellenlängenbereiche. Mithilfe der Animation kann das Verständnis zu Wellenlängen vertieft werden. Durch Aktivieren der verschiedenen Wellenlängenbereiche erfahren die Schülerinnen und Schüler, welche Auswirkungen unterschiedliche Wellenlängen auf die Eindringtiefe der Mikrowellen haben. So werden die Wellen des eher kurzwelligen X-Bandes bereits von den Baumkronen zurückgeworfen, während die eher langwelligen Wellen des L-Bandes bis zum Waldboden durchdringen können und erst dort zurückgeworfen werden.
2. Veränderungsdetektion im Braunkohle-Revier
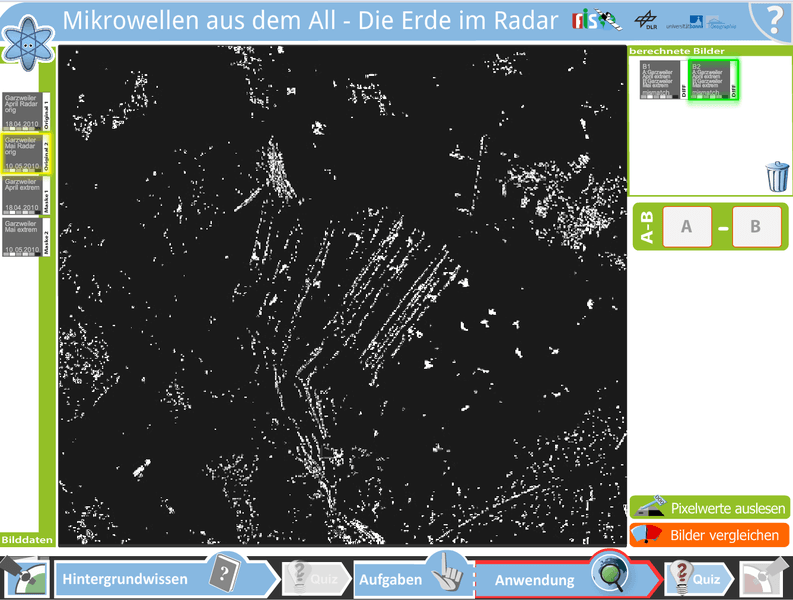
Im zweiten Modulteil stehen den Schülerinnen und Schülern mehrere Einzelbilder zu Verfügung, die zu verschiedenen Monaten aufgenommen wurden. Die aufgenommenen Szenen zeigen das Braunkohle-Abbaugebiet Garzweiler am Niederrhein. Deutlich zu sehen sind die terrassenförmigen Abbruchkanten sowie die Bagger (weiß, im rechten Bereich des Gebietes). Die Schülerinnen und Schüler können selbstständig durch Aktivieren der verschiedenen Bilder die Veränderungen der Grube sowie der Position der Bagger detektieren. Durch Ziehen der Bilder in die Formel A - B kann die Veränderung pixelweise berechnet werden.
Haben die Schülerinnen und Schüler die Veränderungsdetektion durchgeführt und die gestellten Aufgaben beantwortet, können sie durch Beantworten der Fragen im zweiten Quiz die Bearbeitung des Moduls abschließen.
Zurück
- Die Erde im Radar: Mikrowellen aus dem All
Über diesen Link gelangen Sie zurück zur Startseite der Unterrichtseinheit "Die Erde im Radar".