Hinweis zum Unterrichtsverlauf und Materialien
Die Unterrichtseinheit besteht aus drei Teilen: 1. Entdeckung an den Feuerbachpunkten und Formulierung des Satzes über den Feuerbachkreis, 2. Vorbereitung der Beweise, 3. Beweis des Satzes über den Feuerbachkreis.
Formulierung des Satzes über den Feuerbachkreis
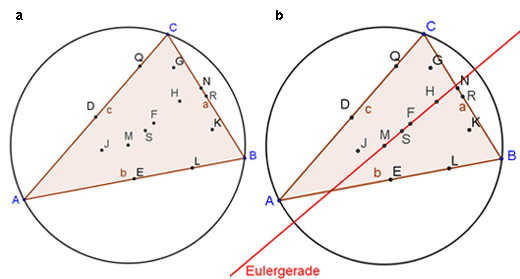
Im ersten Teil der Unterrichtsreihe (zwei Stunden) sollen die Schülerinnen und Schüler (gegebenenfalls mithilfe einer Dynamischen Geometriesoftware, hier GeoGebra) die Gesetzmäßigkeiten der Lage der Feuerbachpunkte und der Eulerpunkte (Abb. 1) entdecken und formulieren. Die neun Feuerbachpunkte liegen vermutlich auf einem Kreis, dem Feuerbachkreis. Jeweils drei Punkte haben die gleiche Eigenschaft:
- Drei Punkte liegen auf den Seitenmitten.
- Drei Punkte liegen auf den Höhenfußpunkten.
- Drei Punkte liegen auf den Mitten zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks.
Damit lässt sich die Aussage des Satzes von Feuerbach formulieren. Abb. 1a (Screenshot der GeoGebra-Datei "feuerbach_euler_punkte.ggb") zeigt alle Feuerbachpunkte und die Punkte zur Eulergeraden, wie sie den Schülerinnen und Schülern vorgelegt wird. Außerdem gibt es noch vier Punkte, die auf einer Geraden liegen, der Eulergeraden (Abb. 1b, Screenshot der GeoGebra-Datei "euler_gerade.ggb").
Materialien
- einfuehrung_arbeitsmaterial_feuerbach.pdf
Aufgaben und Lösungshinweise
VorschauIm Classroom-Manager speichern - einfuehrung_geogebra_dateien_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie (debug link record:lo_unit:tx_locore_domain_model_unit:103887) (kostenfrei).
Im Classroom-Manager speichern
Vorbereitung des Beweises des Satzes über den Feuerbachkreis
Suche nach Beweisansätze in Arbeitsgruppen
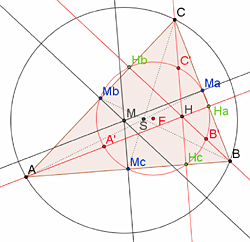
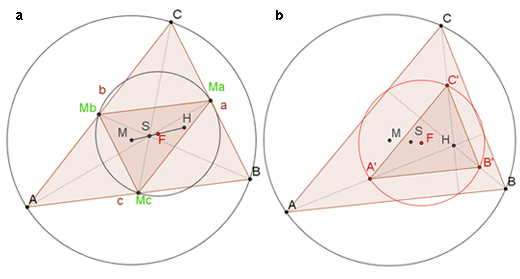
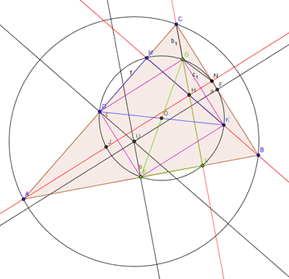
Im zweiten Teil der Unterrichtsreihe (eine Stunde) wird nach Beweisansätzen gesucht. Die Klassifizierung der Punkte (Seitenmitten, Höhenfußpunkte, Punkte auf den Mitten zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks) führt nicht direkt weiter, da die dadurch entstandenen Kreise nicht identisch sein müssen. Abb. 2 (Screenshot der Datei "loesung_feuerbach_euler_punkte.ggb") zeigt, wie die Schülerinnen und Schüler mit Bleistift und Papier oder mit GeoGebra die Feuerbachpunkte konstruieren und somit den mathematischen Hintergrund entdecken können. Sinnvolle "regelmäßige" Figuren sind meist Hilfen für einen Beweisansatz in Geometrie. Deshalb suchen die Schülerinnen und Schüler nach weiteren sinnvollen Figuren innerhalb der Feuerbachpunkte, die für einen Beweis nützlich sein könnten [Abb. 3: Screenshots der Dateien "(MaMbMc)abb.ggb" und "(A'B'C')abb.ggb"; Abb. 4: "beweis_feuerbach_kreis.ggb"].
Einsatz der Materialien
Die Unterrichtsreihe soll für die Schülerinnen und Schüler ganz offen gelassen werden, das heißt, die Arbeitsmaterialien müssen in einer starken Lerngruppe gar nicht zum Einsatz kommen. Die Materialien haben zwei Funktionen: Sie dienen zur Information der Lehrperson und kommen dann zum Einsatz (gegebenenfalls nach Entscheidung der Lehrperson auch nur Teile des Materials), wenn die Schülerinnen und Schüler nicht weiter kommen. Ebenso ist mit den vorgegebenen Lösungsansätzen zu verfahren. Will man alle Beweisideen weitertreiben, können entsprechende Arbeitsgruppen gebildet werden.
1. Materialien zur Vorbereitung des abbildungsgeometrischen Beweises
Die Lernenden können spezielle Vielecke entdecken, die sich aus Feuerbachpunkten zusammensetzen. Das können zum Ursprungsdreieck ähnliche Dreiecke sein, Rechtecke oder Parallelogramme. Ähnliche Dreiecke führen auf einen abbildungsgeometrischen Beweis.
Download
- 1_arbeitsmaterial_feuerbach.pdf
Aufgaben und Lösungshinweise
VorschauIm Classroom-Manager speichern - 1_geogebra_dateien_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie GeoGebra.
Im Classroom-Manager speichern
2. Materialien zur Vorbereitung des elementargeometrischen Beweises
Rechtecke oder Parallelogramme führen auf einen elementaren Beweis. (Von den Parallelogrammen ist wegen der Komplexität des Beweises abzuraten.)Download
- 2_geogebra_dateien_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie GeoGebra.
Im Classroom-Manager speichern
3. Materialien zur Vorbereitung des kinematischen Beweises
Weiterhin kann eine Gruppe gebildet werden, die sich ein bewegtes GIF (2_2_animation_gross.gif) anschaut, das auf die Definition des Geometrischen Ortes des Feuerbachkreises und einen kinematischen Beweis führt.Download
- 3_animation_gross.gif
Animiertes GIF
Im Classroom-Manager speichern - 3_geogebra_dateien_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie GeoGebra.
Im Classroom-Manager speichern
Beweis des Satzes über den Feuerbachkreis
Beweis und Präsentation
Die Beweise werden eigenständig oder auf der Grundlage der Arbeitsmaterialien in Gruppen erarbeitet (zwei bis drei Stunden) und präsentiert (ein bis zwei Stunden).1. Materialien zum abbildungsgeometrischen Beweis
- 1_loesungsmaterial_feuerbach.pdf
Lösung zum abbildungsgeometrischen Beweis
VorschauIm Classroom-Manager speichern - 1_loesungen_geogebra_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie GeoGebra.
Im Classroom-Manager speichern
2. Materialien zum elementargeometrischen Beweis
- 2_loesungsmaterial_feuerbach.pdf
Lösung zum elementaren Beweis über Rechtecke
VorschauIm Classroom-Manager speichern - beweis_feuerbach_kreis.ggb
Für die Nutzung der Datei benötigen Sie GeoGebra.
Im Classroom-Manager speichern
3. Materialien zum kinematischen Beweis
- 3_loesungsmaterial_feuerbach.pdf
Lösung zum kinematischen Beweis
VorschauIm Classroom-Manager speichern - 3_geogebra_dateien_feuerbach.zip
Für die Nutzung der Dateien benötigen Sie GeoGebra.
Im Classroom-Manager speichern