Über mathematische Probleme chatten
Der Artikel gibt einen Einblick in ein Projekt zum Chatten im Mathematikunterricht der Primarstufe. Dieses wurde initiiert, um einen Zugang zu schriftlichen Produkten der Schülerinnen und Schüler im mathematischen Problemlöseprozess zu erhalten.
Szenen aus dem Forschungsprojekt sind als Beispiele in der vom Autor verfassten Dissertation mit dem Titel "Semiotische Prozess-Karten - Chatbasierte Inskriptionen in mathematischen Problemlöseprozessen" (Schreiber, 2010) verwendet worden. Dabei beschränkt sich der Einblick in diesem Artikel auf die Beschreibung des Chat-Settings und auf Hintergrundinformationen zu diesem Setting. Darüber hinaus werden Perspektiven zum Forschen mit digitalen Medien im mathematikdidaktischen Bereich gegeben.
Motivation
Schriftliche Fixierungsmöglichkeiten
Beweggrund für die Umsetzung des Projekts "Mathe-Chat" war zunächst die Einsicht aus einem vorausgegangenen Projekt zum Argumentieren im Mathematikunterricht der Grundschule (Krummheuer 1997). Dort wird mit Blick auf die rekonstruierten narrativen Argumentationen von Grundschulkindern in ihren kollektiven Bemühungen bei Aufgabenbearbeitungsprozessen gefordert, schriftliche Fixierungsmöglichkeiten stärker zu beachten.
Festhalten des Bearbeitungsweges
"Ausgangspunkt ist hierbei das in den Episoden häufiger angesprochene Phänomen der ausschließlich verbalen Orientierung der narrativen Interaktionen. Zum einen wegen der Flüchtigkeit und zum anderen wegen der situativen Einzigartigkeit verbaler Äußerungen wird der Nachvollzug [...] erschwert [...] Für den leichteren gedanklichen Nachvollzug [...] wäre zum Beispiel eine schriftliche Fixierung nicht nur des Ergebnisses, sondern auch vor allem des Bearbeitungsweges eine Hilfe" (Krummheuer 1997: 98).
Schriftlich-grafische Kommunikation
Dabei ginge es darum, dass "die Kinder selbst eine produktive Form der schriftlichen Präsentation ihrer Gedanken finden" (ebd.). Krummheuer weist auf die besondere Schwierigkeit hin, Möglichkeiten der "schriftlichen Veräußerung" zu finden, die auch für andere Schülerinnen und Schüler einen Nachvollzug ermöglichen und als Adressaten nicht in erster Linie die Lehrperson ansprechen. Dies ist nun im Projekt "Mathe-Chat" derart realisiert, dass sich die Kommunikation aller am Chat beteiligten Kinder oder Gruppen ausschließlich via schriftlich-grafischer Darstellungen vollzieht.
Schriftlichkeit in der Mathematik
Mathematische Kommunikation und Verschriftlichung
In der Auseinandersetzung mit der Problematik des Verschriftlichens in der mathematischen Unterrichtskommunikation wird deutlich, dass man eine relativ hohe Abhängigkeit mathematischer Kommunikation von schriftbasierten Fixierungen überhaupt annehmen muss. Das Geschriebene übernimmt dabei nicht nur die Funktion der Konservierung von Aussagen oder Aspekten des Bearbeitungsprozesses. Es ist darüber hinaus wohl meistens gar nicht möglich, über mathematische Sachverhalte zu kommunizieren, ohne dabei etwas schriftlich aufzuzeichnen.
Darstellung und Darstellungsweise
Die Abhängigkeit der Darstellung von der Wahl der Darstellungsweise ist möglicherweise in keiner anderen Wissenschaft so groß wie in der Mathematik. Dies hat damit zu tun, dass in vielen mathematischen Verfahren die Darstellungen selbst als die mathematische Idee oder Prozedur genommen werden kann und nicht ausschließlich als deren Repräsentation in Form eines Symbols oder Zeichens verstanden werden muss.
Besonderheit mathematischer Symbole
Lesen wir beispielsweise das Wort "Baum", so ist uns allen klar, dass dieses Wort nicht wirklich ein Baum ist, sondern ein solches Objekt als Symbol oder Zeichen repräsentiert. Sehen wir dagegen das Wort (oder Zeichen) "5", so können wir unbeschadet diese "5" auch als den Gegenstand "5" nehmen. Vor allem diese epistemologische Besonderheit mathematischer Symbole führt dazu, dass Darstellungsweisen in der Mathematik einerseits beliebig erscheinen und andererseits in ihrer Wahl und spezifischen Konstruktion in einer einzigartigen Weise das jeweilige mathematische Objekt (mit-)konstituieren.
Schriftliche Produkte im Problemlöseprozess
Über diesen Aspekt der Schriftbasiertheit von Mathematik hinaus ist noch ein weiterer zu beachten: Beim Problemlösen im Sinne eines Erforschens und Entdeckens mathematischer Aussagen und Zusammenhänge wird in konstitutiver Weise mit und an Verschriftlichungen gearbeitet. Für die schriftlichen Produkte der Schülerinnen und Schüler im Problemlöseprozess wird auf den von Latour und Woolgar (1986) stammenden Begriff der "Inskription" zurückgegriffen. Latour und Woolgar untersuchen die Entstehung und Entwicklung von Wissen bei Forschungsprozessen in Laboratorien. Die verschiedenen Arten von Modellen, Bildern, Ikonen und Notationen, die in diesen Laboratorien genutzt werden, bezeichnen Latour und Woolgar zusammenfassend als "inscriptions". Der Begriff ist weiter gefasst als andere oft in diesem Zusammenhang verwendeten wie beispielsweise Notation, Darstellung, Verschriftlichungen und trifft den untersuchten Gegenstand, nämlich alle schriftlich-grafischen Produkte im Chat, genauer.
Umsetzungsbeispiel
Das von der Müller-Reitz-Stiftung geförderte Projekt "Pilotstudie zur Chat-unterstützten Erstellung mathematischer Inskriptionen unter Grundschülern" wurde unter der Leitung von Professor Krummheuer vom Autor durchgeführt.
Gegenstände der Studie
Drei zentrale Fragestellungen
Chatten über mathematische Probleme ist eine im schulischen Umfeld auch heute kaum genutzte Art der Aufgabenbearbeitung. Es stellt sich für die Lernenden hierbei das grundsätzliche Problem der schriftlich-grafischen Darstellung ihrer Lösungsbemühungen. In der Studie soll untersucht werden, inwieweit Schülerinnen und Schüler für ihre eigenen Lernprozesse Inskriptionen einsetzen und neu entwerfen, in welcher Weise damit ein kollektiver Aufgabenbearbeitungsprozess strukturiert wird und inwieweit diese Strukturierung den Bearbeitungsprozess bestimmt.
Inskriptionen im Mathematikunterricht
Das Interesse richtet sich auf das detaillierte empirische Studium des inskriptionalen Aspekts in mathematischer Unterrichtsinteraktion. Im hier verwendeten Untersuchungsdesign sollen die Schülerinnen und Schüler inskriptionsbasiert interagieren. Durch den experimentellen Charakter der Chatumgebung werden theoretische und methodologische Fragen zur Verwendung von Verschriftlichung im Mathematikunterricht in verschärfter Form erkennbar. Es wird ausdrücklich nicht der Anspruch erhoben, hier eine zukunftsweisende oder zu empfehlende Lernumgebung empirisch zu erproben.
Durchführung und Auswertung
Aufzeichung der Sitzungen und Erstellung von Transkripten
In der Durchführung an Schulen bearbeiten Grundschulkinder gemeinsam via Chat an Computern mit Touchscreens und mit der Software NetMeeting mathematische Probleme. Der Verlauf dieser Chat-Sitzungen wird mit der Software Camtasia-Studio aufgezeichnet. Zur Auswertung der Chat-Sitzungen werden zu ausgewählten Sequenzen einzelner Chat-Sitzungen Transkripte erstellt. Diese werden mit Methoden der Interpretativen Unterrichtsforschung (Krummheuer & Naujok, 1999) ausgewertet.
Auswertung anhand von Screen-Video-Aufzeichnungen
Hierbei musste diese Methode so weiterentwickelt wurde, dass sie dem besonderen Status der Chat-Kommunikation gerecht werden. Die Chat-Serien wurden gemeinsam mit Studierenden des Lehramts an Grundschulen am Institut für Didaktik der Mathematik theoretisch und methodisch vorbereitet, an Grundschulen in Frankfurt durchgeführt und später anhand der von Screen-Video-Aufzeichnungen erstellten Transkripte detailliert ausgewertet.
Interaktion der Lernenden unter Chat-Bedingungen
Mündliche und schriftliche Aspekte
Mit dem Chatting liegt eine Interaktionsform vor, die einerseits auf Schrift und Grafik beruht, andererseits durch ihre hohe Interaktivität eher der zwischenmenschlich-verbalen Interaktion ähnelt. Um das Chatten als Kommunikationsform einzuordnen, wurde die von Koch und Oesterreicher ausgearbeitete Unterscheidung zwischen der "konzeptionellen" und der "medialen" (1985: 17) Ebene von Mündlichkeit und Schriftlichkeit genutzt.
Konzeptionelle und mediale Ebenen
Diese beschreiben das Chatten als eine Kommunikationsform, die auf der konzeptionellen Ebene typische Merkmale von Mündlichkeit aufweist, während die mediale Ebene eine schriftliche Sprachform darstellt. Auf der konzeptionellen Ebene wird von Koch und Oesterreicher jeweils graduell differenziert, zum Beispiel nach Vertrautheit sowie zeitlicher Situierung. Die Begriffe "mündlich" und "schriftlich" stellen auf konzeptioneller Ebene die "Endpunkte eines Kontinuums" (1994: 587) dar. Die mediale Ebene ist dichotomisch, das heißt die Kommunikation gestaltet sich entweder schriftlich oder mündlich.
Chat als "getipptes Gespräch"
Dürscheid greift den Ansatz von Koch und Oesterreicher auf und differenziert diesen für die neuen populären Kommunikationsformen wie Chat, Short-Message-Service (SMS) und Instant-Messaging (IM) weiter aus. Sie beschreibt den Chat als getipptes Gespräch, grenzt es aber vom dialogischen Text ab. Ermöglicht wird dies durch eine quasisynchrone Kommunikation in einem gemeinsamen, elektronisch erzeugten Kommunikationsraum (Dürscheid 2003: 41).
"Chatbox" und "Whiteboard" in NetMeeting
Verschiedene Formen der Dateneingabe
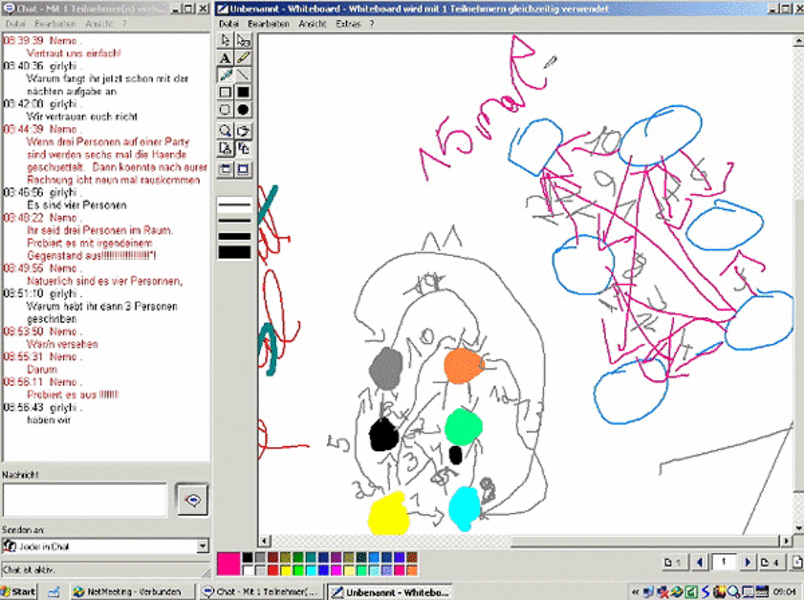
In dem verwendeten Programm NetMeeting nutze ich für das Projekt die Möglichkeit, Daten am Computer in zwei verschiedenen Formen einzugeben: In der "Chatbox" erscheint mithilfe der Tastatur geschriebener alphanumerischer Text (Abb. 1, linker Teil). Auf dem "Whiteboard" wird mit einem speziellen Stift gezeichnet (Abb. 1, rechter Teil). Hierzu steht das bei Grafikprogrammen übliche Grafiktableau von Eingabehilfen zur Verfügung. Chatbox und Whiteboard lassen sich in NetMeeting als zwei Fenster nebeneinander anordnen. Von jedem der beiden verbundenen Computerplätze kann auf diese Daten reagiert und geantwortet werden.
"Quasisynchrone" Kommunikation im Chatbox-Bereich
Die Kommunikation im Chatbox-Bereich läuft in der Terminologie von Dürscheid "quasisynchron" (2003: 44): Die Nachrichten müssen geschrieben und zur Veröffentlichung abgesendet werden. Bis zu dieser Versendung sind sie für die anderen Chat-Teilnehmer nicht sichtbar. Die Nachricht wird in einem Eingabefenster geschrieben und kann vom Eingebenden vor dem Verschicken verändert oder gelöscht werden. Nach dem Versenden steht die Nachricht unter Angabe des Autors und des Absendezeitpunkts auf allen am Chat beteiligten Computern in der Chatbox. Sie kann jetzt nicht mehr verändert werden. Entsprechend kurztaktig verwendet, kann auf diese Weise eine quasisynchrone Kommunikation entstehen.
Synchrone Kommunikation im Whiteboard-Bereich
Im Whiteboard-Bereich verläuft die Kommunikation dagegen synchron, das heißt jede Aktion auf dem Whiteboard ist zeitgleich auf dem Whiteboard der anderen Chat-Teilnehmer zu sehen. Auch eventuelle Korrekturen, die vom Autor der Nachricht vorgenommen werden, sind während des Korrekturprozesses sichtbar. Außerdem ist die veröffentlichte Grafik zur Bearbeitung für alle Teilnehmerinnen und Teilnehmer zugänglich. So wird insbesondere dieser Teil des verwendeten Chat-Settings zur Plattform für die Erstellung von gemeinsamen Zeichnungen, Diagrammen, Zahlenfolgen oder ähnlichem. Die Einträge in der Chatbox wie auch im Whiteboard werden zusammenfassend als "Inskriptionen" bezeichnet.
Durchführung der Chatsitzungen
Die Schülerinnen und Schüler arbeiteten jeweils alleine oder zu zweit in zwei getrennten Räumen und hatten die Vorgabe, mehrere Aufgaben auf den vorher eingerichteten Whiteboards zu lösen. Die Lösung sollte nicht etwa in Konkurrenz zur anderen Gruppe, sondern in Kooperation mit dieser erarbeitet werden. Dazu gab es den Hinweis, dass sowohl das Whiteboard als auch die Chatbox zur Kommunikation mit der anderen Gruppe dienen. Weitere Hilfsmittel - insbesondere Blätter oder Stifte - waren nicht vorhanden und sollten auch keinesfalls hinzugezogen werden. Die Sitzungen dauerten in der Regel 40 bis 60 Minuten. In dieser Zeit wurden in aller Regel zwei bis fünf Aufgaben gemeinsam gelöst. Das Ende der einzelnen Aufgaben wurde von den Schulkindern bestimmt und durch Weiterblättern oder durch Absprache in der Chatbox oder auf dem Whiteboard vereinbart. Durch das "Umblättern" gelangte man dann zur nächsten eingerichteten Whiteboardseite.
Perspektiven zu weiteren Forschungen
Mathe-Chat in der virtuellen Lernumgebung
Für die mathematikdidaktische Forschung wäre die Verbindung des Bereichs kooperativer Arbeitsformen mit dem Bereich der digitalen Medien vielversprechend. Dazu bietet sich die am Institut für Didaktik der Mathematik und Informatik im Rahmen des Projektes Lehr@mt (Schreiber, 2006b) erstellte Lernumgebung WiLM@ (Reinhard, 2009) hervorragend an. In dieser virtuellen Lernumgebung wird die Idee des Mathe-Chat unter neuen und technisch erweiterten Bedingungen fortgesetzt. In der Kombination von synchroner, quasisynchroner und auch asynchroner Kommunikation wird gemeinsam an mathematischen Aufgaben gearbeitet. Dabei bestimmt der Ersteller einer Lösung oder eines Lösungsansatzes, wann er diese für eine Gruppe oder für die ganze Klasse öffentlich macht und zur gemeinsamen (Weiter-)Bearbeitung zur Verfügung stellt. Es kann nicht nur von der Lehrkraft, sondern auch von den Schülerinnen und Schülern selbst der Prozess der Entstehung der Inskription durch "Ziehen" an einer "Zeitleiste" nachvollzogen werden.
Rein verbale Darstellung mathematischer Sachverhalte
Auch ein Projekt, das sich im Gegensatz zum Mathe-Chat mit rein verbaler Darstellung mathematischer Sachverhalte beschäftigt, wäre sicherlich Erkenntnis bringend. Hier könnte aus dem Bereich der digitalen Medien die Möglichkeit genutzt werden, über die Herstellung von Audio-Podcasts eben gerade nur die verbale Darstellung zu ermöglichen. Die Nutzung schriftlich-graphischer Elemente wäre dann unterbunden. Dabei kann besonders die Erstellung der Podcasts - erst ungeplant, also eher spontan, und dann zum gleichen Thema mit einer Art "Drehbuch" oder "Manuskript" - von Interesse sein.
Literaturverzeichnis
Dürscheid, Christa (2003). "Medienkommunikation im Kontinuum von Mündlichkeit und Schriftlichkeit. Theoretische und empirische Probleme". In: Zeitschrift für Angewandte Linguistik 38. 37-56.
Koch, Peter und Wulf Oesterreicher (1985). "Sprache der Nähe - Sprache der Distanz. Mündlichkeit und Schriftlichkeit im Spannungsfeld von Sprachtheorie und Sprachgeschichte". In: Romanistisches Jahrbuch. Berlin, New York: Walter de Gruyter. 15-43.
Koch, Peter und Wulf Oesterreicher (1994). "Schriftlichkeit und Sprache". In: Günther, Hartmut und Otto Ludwig (Hrsg.). Schrift und Schriftlichkeit. Ein interdisziplinäres Handbuch internationaler Forschung. Berlin, New York: Walter de Gruyter. 587-604.
Krummheuer, Götz (1997). Narrativität und Lernen. Mikrosoziologische Studien zur sozialen Konstitution schulischen Lernens. Weinheim: Deutscher Studien Verlag.
Krummheuer, Götz und Natascha Naujok (1999). Grundlagen und Beispiele Interpretativer Unterrichtsforschung. Opladen: Leske und Budrich.
Latour, Bruno und Steve Woolgar (1986). Laboratory life. The construction of scientific facts. 2nd edition. Princeton: Princeton University Press.
Schreiber, Christof (2010). "Semiotische Prozess-Karten - Chatbasierte Inskriptionen in mathematischen Problemlöseprozessen". In: Krummheuer, Götz und Aiso Heinze (Hrsg.). Empirische Studien zur Didaktik der Mathematik, Band 4. Münster und andere: Waxmann.
Schreiber, Christof (2006a). "Die Peirce'sche Zeichentriade zur Analyse mathematischer Chat-Kommunikation". In: Journal für Mathematikdidaktik 27:3/4. 240-267.
Schreiber, Christof (2006b). "Projekt Lehr@mt - Medienkompetenz in der Lehrerbildung". In: Beiträge zum Mathematikunterricht. Hildesheim: Franzbecker. 481-484.