Themen und Verlauf der Unterrichtseinheit

Die Schülerinnen und Schüler erstellen mit POV-Ray Konstruktionen zu den Themen Verpackung einer Kugel im Oktaeder, dichteste Kugelpackung und Platonische Körper.

Verpackung einer Kugel im Oktaeder

Kegel-Kugel-Kombination

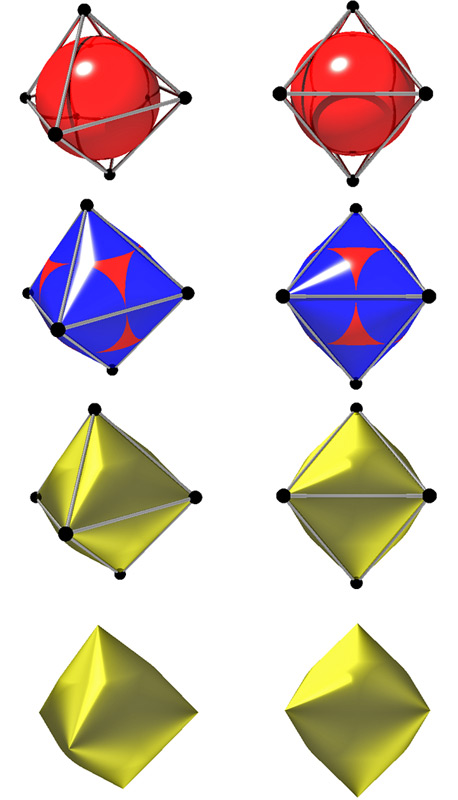
Der Körper entsteht durch geschicktes Aufsetzen von Kegeln auf eine Kugel. Hierdurch entstehen glatte Übergänge, so dass die paarweise Verbindung von je zwei Kegelspitzen einen neuen Körper (Oktaeder) entstehen lässt, in dem die Kegel-Kugel-Kombination "nahtlos verpackt" ist. Abb. 1 (Platzhalter bitte anklicken) zeigt die Zwischenschritte der Konstruktion mit der POV-Ray-Software (siehe Arbeitsblatt "geometrie_mit_povray.pdf").

Variation der Aufgabenstellung

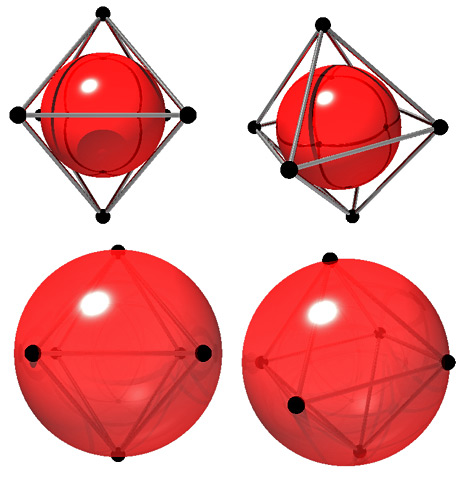
Eine Variation erfolgt durch die Frage nach Kugeln innerhalb beziehungsweise außerhalb des Oktaedergitters, deren Oberfläche nicht die Kanten, sondern die Seiten beziehungsweise die Ecken des Oktaeders berührt (Abb. 2). Dadurch werden erneut die räumliche Vorstellungskraft der Schülerinnen und Schüler sowie ihr Umgang mit POV-Ray trainiert.

Die dichteste Kugelpackung

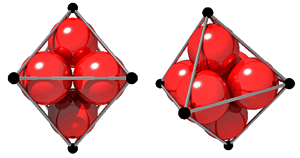
Die Frage nach einem "dichten" Ausfüllen des Oktaeder-Gitters mit sechs kleinen Kugeln führt nach der geometrischen und computergrafischen Lösung auf die mathematisch hoch aktuelle Frage nach der dichtesten Kugelpackung. Bisher gibt es nur einen Computerbeweis von Thomas C. Hales aus dem Jahr 1998, von dessen Richtigkeit man bislang aber "nur" zu 99 Prozent überzeugt ist. Man schätzt, dass die Erstellung eines rein formalen Beweises noch etwa zwanzig Jahre dauern wird. Die Schülerinnen und Schüler sollen hierzu selbstständig recherchieren, ihre Funde präsentieren und eine dieser Packungen mit POV-Ray realisieren (Abb. 3).

Mathematik bei Platon

Im Folgenden geht es weiter mit dem Oktaeder als Platonischem Körper. Die Tatsache, dass es nur fünf Platonische Körper gibt, soll anhand des Originalbeweises aus Euklids Elementen nachvollzogen werden. Schließlich beschäftigen sich die Lernenden auf einem separaten Arbeitsblatt (mathematik_bei_platon.pdf) mit einem Auszug aus Platons "Der Staat", worin sich Aufschlüsse über Platons Philosophie und insbesondere die Sicht auf die Mathematik gewinnen lassen, die erklären, warum Euklid keine Anwendungen der Mathematik in seine Elemente aufgenommen hat.

Eulersche Polyederformel

Die fünf platonischen Körper

Den Abschluss der Unterrichtseinheit bildet der Auftrag, sich über die Eulersche Polyederformel zu erkundigen und sie anhand der Platonischen Körper zu illustrieren. Mit POV-Ray lassen sich durch vorimplementierte Funktionen dann auch noch zügig die fünf regulären Polyeder erzeugen (Abb. 4).

Förderung der "scientific literacy"

Diese "Spiele" mit Kugel, Kegel und den Platonischen Körpern sollen die Schülerinnen und Schüler ermuntern, selbstständig auf weitere Entdeckungsreisen zu gehen. Insbesondere die Beschäftigung mit mathematikhistorischen und -philosophischen Originaltexten soll die Lernenden "abseits" der reinen Rechenmathematik für das Wesen dieser Wissenschaft gewinnen. Zudem ist es erstaunlich, wie leicht mathematikphilosophische Originaltexte aufgrund ihrer Prosa- beziehungsweise Dialogform verständlich sind!